Implikationen erkennen (IMP)

Kurzinfo zum Aufgabentyp

Bei dieser Aufgabe werden zwei logische Aussagen in Form von kurzen Sätzen vorgegeben.
Du musst überprüfen, welche Schlussfolgerungen sich aus diesen Aussagen ableiten lassen.

 

Kostenlose Übungsaufgaben

Level 1-2, vorwiegend einfache und mittelschwere Übungsaufgaben   hier starten

 

 

Kompakter Online-Vorbereitungskurs
"Implikationen erkennen"

Dieser kompakte Online-Vorbereitungskurs hat das Ziel, dich möglichst schnell auf die Implikationen-Aufgaben des MedAT vorzubereiten. Er vermittelt eine Vorgehensweise, die auf ein möglichst kleines Fehlerpotential hin entworfen wurde und besteht aus 6 Abschnitten. Zum Durcharbeiten aller Abschnitte mit Erläuterungen und Übungsaufgaben brauchst du etwa 3 Stunden.

 

Abschnitt 1:
Grundlegendes zum Aufgabentyp

Beim "Implikationen erkennen" werden zwei logische Aussagen in Form von kurzen Sätzen vorgegeben.
Du musst überprüfen, welche Schlussfolgerungen sich aus diesen Aussagen ableiten lassen.

Beispielaufgabe

Aussage 1: Alle A sind B.
Aussage 2: Alle B sind keine C.

Antwortmöglichkeiten (1 richtig)
a) Einige A sind keine C.
b) Einige A sind C.
c) Alle A sind keine C.
d) Alle A sind C.
e) Keine Antwort ist richtig.

 

Abschnitt 2:
Aussagesätze als Mengendiagramm darstellen

Zunächst fällt auf, dass beiden Aussagesätze nach dem gleichen Schema aufgebaut sind:

(Einige / Alle) A (sind / sind keine) B.

Somit ergeben sich für den Aufbau eines Aussagesatzes folgende 4 Möglichkeiten:
Einige A sind B.
Einige A sind keine B.
Alle A sind B.
Alle A sind keine B.

Jede dieser Möglichkeiten kann in einem Mengendiagramm veranschaulicht werden:

 

 

 

 

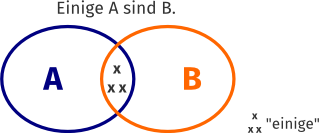
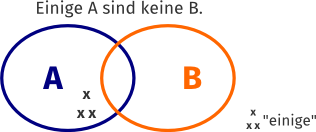
Abschnitt 3 (zum Verständnis):
Inhaltlich/logisch identische Aussagen erkennen

Manchmal gibt es mehrere Formulierung für die gleiche logische Aussage.

Es sind identisch:

a)
"Einige A sind B."
und
"Einige B sind A."

 

 

b)
"Alle A sind keine B."
und
"Alle B sind keine A."

 

 

Somit können in diesen beiden Aussagesätzen die Mengen vertauscht werden (dies gilt nicht für die anderen zwei der im Abschnitt 1 genannten Aussagesätze).

 

Abschnitt 4:
Aus Mengendiagrammen Folgerungen ziehen

Schritt 1: Beide Aussagesätze in Mengendiagramme umsetzen

Zunächst formt man beide Aussagesätze separat in Mengendiagramme um (siehe Abschnitt 2).

Schritt 2: Kombination beider Mengendiagramme

Dann betrachtet man die erste Antwortmöglichkeit und überlegt sich, ob sich diese aus der Kombination beider Aussagen/Skizzen ableiten lässt. Diesen Schritt wiederholt man für jede Antwortmöglichkeit.

Beispiel

Aussage 1: Alle A sind B.
Aussage 2: Alle B sind keine C.

 

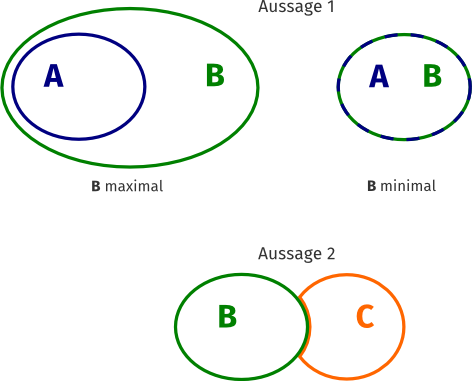
Antwortmöglichkeit  

(1) Einige A sind keine C.

Folgerung lässt sich ableiten, jedoch gibt es eine noch weitergehende richtige Folgerung (Antwortmöglichkeit 3)

A ist Teilmenge von B [nach Aussage 1].
Alle B sind keine C [nach Aussage 2].
Folglich sind alle A keine C.

(2) Einige A sind C.

Falsch (Folgerung lässt sich nicht ableiten).

Begründung: siehe Antwortmöglichkeit 1

(3) Alle A sind keine C.

Richtig (Folgerung lässt sich ableiten).

Begründung: siehe Antwortmöglichkeit 1

(4) Alle A sind C.

Falsch (Folgerung lässt sich nicht ableiten).

Begründung: siehe Antwortmöglichkeit 1

(5) Keine Antwort ist richtig.

 Falsch (da sich Antwortmöglichkeit 3 ableiten lässt).

Weiteres Beispiel: siehe Seitenende

 

Abschnitt 5:
Erstes Anwenden dieser Strategie

Nun kannst Du die Strategie an 15 kostenlosen Übungen ausprobieren: LINK

 

Abschnitt 6:
Intensives Einüben an vielen Übungsaufgaben

Nachdem Du die Vorgehensweise an einigen Übungen angewendet hast, kannst Du nun an Geschwindigkeit und Fehlerfreiheit arbeiten.
Hierfür haben wir für Dich in einem Aufgabenpaket 1000 Aufgaben zusammengestellt.
Dieses Aufgabenpaket enthält die unterscheidlichsten Implikationsaufgaben, sodass du möglichst viele Kombinationen von Aussagesätzen schon einmal gelöst hast.

VORBEREITUNGSPAKET BESTELLEN

 

 

 

 

Anhang:
1 weitere ausgearbeitete Beispielaufgabe

Aussage 1: Einige A sind B.
Aussage 2: Alle C sind B.
 

 

Antwortmöglichkeit  

(1) Alle C sind keine A.

Falsch (Folgerung lässt sich nicht ableiten).

B enthält einige A [nach Aussage 1].
C ist Teilmenge von B [nach Aussage 2], jedoch gibt es keine Aussage ob diese Teilmenge auch Elemente aus A enthält.
Folglich kann keine Aussage gemacht werden, ob oder wie viele A-Elemente die Menge C enthält.

(2) Einige C sind A.

Falsch (Folgerung lässt sich nicht ableiten).

Begründung: siehe Antwortmöglichkeit 1

(3) Alle C sind A.

Falsch (Folgerung lässt sich nicht ableiten).

Begründung: siehe Antwortmöglichkeit 1

(4) Einige C sind keine A.

Falsch (Folgerung lässt sich nicht ableiten).

Begründung: siehe Antwortmöglichkeit 1

(5) Keine Antwort ist richtig.

 Richtig (da sich keine der anderen Antwortmöglichkeiten ableiten lässt).